- BARYCENTRE
- BARYCENTREBARYCENTRESoit A un espace affine attaché à un espace vectoriel E (sur un corps commutatif K). On appelle «point M de A affecté de la masse» l’élément (M, ) de l’ensemble A 憐 K.Par définition, le barycentre de n points M1, M2, ..., Mn de A affectés des masses1,2, ...,n de somme non nulle est le point G tel que:
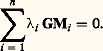De cette définition découlent aisément plusieurs propriétés:1. Pour tout point O de A, on a la relation (équivalente à la condition de définition):
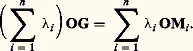2. Le barycentre de la famille (Mi ,i est le même que le barycentre de la famille des (Mi , 見凞i , où 見 est un élément non nul de K.3. Propriété d’associativité: soit G le barycentre de n points M1, M2, ..., Mn de A affectés des masses1,2, ...,n et soit G le barycentre des points M1, M2, ..., Mk affectés des masses1,2, ...,k . Alors G est aussi le barycentre des points G , Mk+1, ..., Mn affectés des masses:
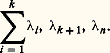Lorsque le corps K est de caractéristique 0 et que les scalairesi sont égaux, le barycentre G s’appelle centre de gravité, ou équibarycentre de la famille des (Mi ,i ).
barycentre [ barisɑ̃tr ] n. m. ♦ Math. Point unique d'un espace affine associé à une collection de points de cet espace affectés chacun d'un scalaire, et défini par extension de la notion de centre de gravité.
● barycentre nom masculin Point G d'un espace affine tel que, si n points A1, A2, …, An sont affectés des coefficients m1, m2,…, mn de somme non nulle,
. (1)
barycentren. m. MATH Centre de gravité dans un espace affine.barycentre [baʀisɑ̃tʀ] n. m.ÉTYM. 1877; de bary-, et centre.❖1 Vx, didact. Centre de gravité. — Fig., plaisant :0 Les services du Sous-Ingénieur principal Miqueut se groupaient au dernier étage de l'immeuble (…) Un couloir central desservait un certain nombre de bureaux (…) Au barycentre trônait Léon-Charles, encadré par René Vidal à droite et Emmanuel Pigeon de l'autre côté.Boris Vian, Vercoquin, p. 73.2 (1928). Mod. Math. Point de l'espace affine, associé fonctionnellement à au moins deux points affectés de coefficients réels, et défini par extension de la notion de centre de gravité, d'inertie.❖DÉR. Barycentrique.
Encyclopédie Universelle. 2012.
